3.3.4 Substitute
The usual source of replacement candidates is a rule set maintained in a persistent list that originates in the Myron distribution. (See §8.1.7 for instructions on how to view and edit the list.) Replacement candidates are also harvested from equations and definitions in the workspace (see §3.3.4.2 and §3.3.4.3). This places substitution rules near the math problem being worked. It also allows preparation of rules for addition to the persistent rule set.
To preserve mathematical integrity, substitutions are limited to replacements that can be proven to be equivalent. This is assumed to be true for rules in the rule set. However, equations added from the workspace to the rule set are subject to an audit, as explained in §3.3.4.5.
3.3.4.1 Using substitution
Here are some situations where substitution makes algebraic manipulation easier.
Working forward. Sometimes when it is difficult to work a particular form of subexpression into a desired expression, it is possible to work from some starting expression forward to the desired expression and then substitute. More concretely, if the expression
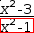
(1)
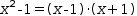
(2)
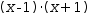
Extracted subexpressions. It is occasionally easier to manipulate a larger expression by replacing certain subexpressions with placeholder terms. After manipulation, substitution can be used to recover the original terms. Consider the expression and selection
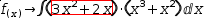
(3)
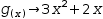
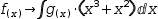
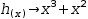
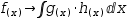
(4)
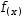
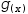
Formulae. The standard equation for speed in terms of time and
accelerating is given by
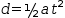
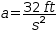
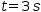
Trigonometric identities. The rule set contains well-known identities used to rearrange trigonometric expressions.
3.3.4.2 Substituting from equations
In addition to the equations in the persistent rule set, any equation in the workspace is treated as an ad hoc unaudited substitution rule. If a selection matches either side of the equation, the other side becomes a candidate.
Matching workspace equations uses two mechanisms: exact matching and, if that fails, pattern matching. With exact matching, two expressions must be identical in every respect. With pattern matching, one expression is treated as a pattern in which every variable that is a single lower-case character is a wildcard. When pattern matching succeeds for one side of a workspace equation, the replacement candidate is generated from the other side by replacing pattern variables with matching subexpressions of the selection. Pattern variables are explained more fully in §9.1.1, but we begin here with an example.
Consider the following equations and expressions where (5) is transformed by distributing its right side into (6).

(5)
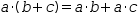
(6)
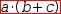
(7)

(8)

(9)
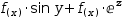
(10)
Now consider equation (11).
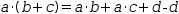
(11)
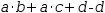
3.3.4.3 Substituting from definitions
The right side of a definition is tested using pattern matching and produces as a candidate the left side with replaced parameter wildcards.

(12)
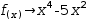
(13)
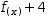
(14)
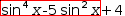
(15)
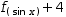
(16)
When the selection is a function reference, as in
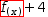
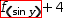
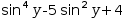
To summarize, substituting a function reference in the presence of an equation succeeds only if the function reference matches exactly one side of the equation; substituting a function reference in the presence of a function definition proceeds using parameter binding instead of pattern binding.
3.3.4.4 Substituting from the rule set
Myron comes with a set of various well-known trigonometric and Boolean identities. The table can be augmented by adding rules from the workspace or loading them from the file system. To view the table, Display Substitutions . On the resulting display, rules can be selected for editing (by transferring them to the workspace) or removal (see §8.1.7).
Substitution always examines all of the persistant rules as well as every non-active expression in the workspace.
3.3.4.5 Persistant rules
Any equation in the workspace can be proposed for addition to the persistent rule set using Expressions Persist . But although any workspace equation can be used as an ad hoc substitution rule, it has to be a proven equivalence to be allowed into the persistant table. To pass the equivalence test, the equation must have an undo list that originates in an identity. Starting from an identity, any number of transformations can be applied to either side of the equation, including transformations that move a subexpression from one side to the other and those that make use of other (proven) substitutions. Since each transformation preserves the equivalence of the equation, the final form represents a valid identity.
A substitution rule in the persistant table can be edited by adding it to the workspace, modifying it and added it back to the persistant table as a new substitution rule. In this case, its provenance is not that of an identity, but since rules originating in the table are assumed to be valid identities any subsequent transformations maintain the identity.
Substitution rules can be added from a file downloaded from the cloud
or from a web site. To add rules from a file, open it in System Files using  . The file must have the extension .xml. The file format is the same
as that used when initializing the persistant table from prepackaged
rules. Here is an example of the file format.
. The file must have the extension .xml. The file format is the same
as that used when initializing the persistant table from prepackaged
rules. Here is an example of the file format.
<?xml version='1.0' encoding='UTF-8' standalone='yes' ?> <substitutions version="3"> <rule>sin x=1÷csc x</rule> <rule>cos x=1÷sec x</rule> ... </substitutions>
See §8.1.7 to see how the persistant substitution list is maintained.